[자료구조] 트리(Tree) 이진 트리(Binary Tree) 트리 순회 (Tree Traversal) (Python)
설명
자료구조는 크게 선형 구조, 비선형 구조로 나눠진다.
선형 구조는 Data를 차례대로 나열시킨 형태를 뜻하고 비선형 구조는 선형 구조가 아닌 모든 형태를 말한다.
즉, 노드와 간선으로 이루어진 그래프(Graph), 그래프 중에서도 순환(Cycle)이 없는 그래프가 나무를 뒤집은 형태로 구성되어있다 해서 이름 붙여진 트리(Tree)가 비선형 구조이다.
그중에서도 이번 강의엔 트리를 설명하겠다.
트리 (Tree)
트리(Tree)란 앞서 말한 대로 나무가 뒤집어진 형태와 비슷해서 트리라 이름 붙어졌다.
트리에 대한 여러 명칭이 있는데 그림을 통해 설명하면 이해가 될 것이다.
해당 그림은 직접 작성한 "쉽게 풀어쓴 자료구조와 알고리즘 기본 가이드"에서 제작한 그림과 유사하게 다시 만들었다.
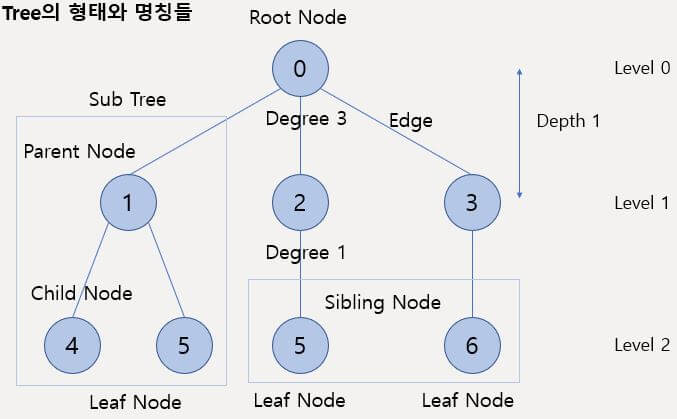
먼저 저 숫자가 들어간 동그라미는 노드(Node)라고 하며 노드를 잇는 선은 간선(Edge)라고 한다.
노드는 Data를 뜻하며 간선은 Data끼리의 연결을 뜻한다.
트리에서의 첫 시작 노드는 뿌리라 해서 루트 노드(Root Node)라 한다.
모든 시작은 이 루트 노드에서 이루어지며 연결 리스트(Linked List)를 알고 있다면 더미 노드(Dummy Node)와 같은 역할이다. (물론 루트 노드는 Data를 갖고 있다는 점이 다르긴 하다.)
연결된 노드를 기준으로 상위에 있는 노드는 부모 노드(Parent Node), 하위에 있는 노드는 자식 노드(Child Node)라 한다.
즉, 루트 노드는 부모 노드가 없고 대부분의 노드는 서로 부모 노드, 자식 노드가 될 수 있으며 제일 끝단의 자식 노드가 없는 노드들은 단말 노드(Leaf Node, 리프 노드)라 한다.
그림에서도 알 수 있듯이 루트 노드를 제외한 모든 노드들은 단 하나의 부모 노드만 가질 수 있고 이 때문에 Cycle이 생기지 않으면서 모든 노드가 연결된다.
또한 하나의 노드에서 자식 노드로 뻗어나가는 간선의 수를 차수(Degree)라고 한다.
각 노드마다 차수는 다를 수 있으며 최대 차수는 하나의 노드가 가지는 최대 간선의 수를 뜻한다.
따라서 해당 그림에서는 루트 노드가 3개의 간선을 가지므로 이 트리는 Degree가 3인 트리라고 할 수 있다.
깊이는 루트 노드에서 해당 노드까지 도달하는데 경유한 간선의 개수를 뜻한다.
또한 Level은 깊이가 동일한 노드들의 집합이다.
Level이 같은 노드들을 형제 노드(Sibling Node)라고 하며 루트 노드의 Level을 정의하는데 다소 차이가 있는 것 같다.
어떤 자료에서는 Level 0부터 시작하고 어떤 자료에서는 Level 1부터 시작하는데 깊이가 기준이 되기 때문에 큰 차이는 없을 것 같다.
다만 Level 1부터 시작한다면 각 노드는 Depth+1=Level이기 때문에 보다 쉬운 이해를 위해 Level 0부터 시작하여 Depth=Level로 맞춰서 글을 작성하였다.
루트 노드를 제외하고 나머지 노드들을 루트 노드로 생각한다면 기존의 트리에서 일부분을 트리로 생각할 수 있다.
이것을 서브 트리(Sub Tree)라고 하며 보통 이진 트리(Binary Tree)에서 왼쪽 서브 트리(Left Sub Tree), 오른쪽 서브 트리(Right Sub Tree)로 구분 짓는다.
보통 알고리즘 문제나 필기 문제로 이진 트리가 나오므로 이진 트리에 대해 설명하겠다.
이진 트리 (Binary Tree)
트리에 대해서 이해가 잘 됐다면 이진 트리는 별거 없다.
이름에서도 알 수 있듯이 트리에서 최대 차수가 2인 트리를 이진 트리라고 하기 때문이다.
물론 이진 트리도 형태에 따라 3가지로 분류한다.
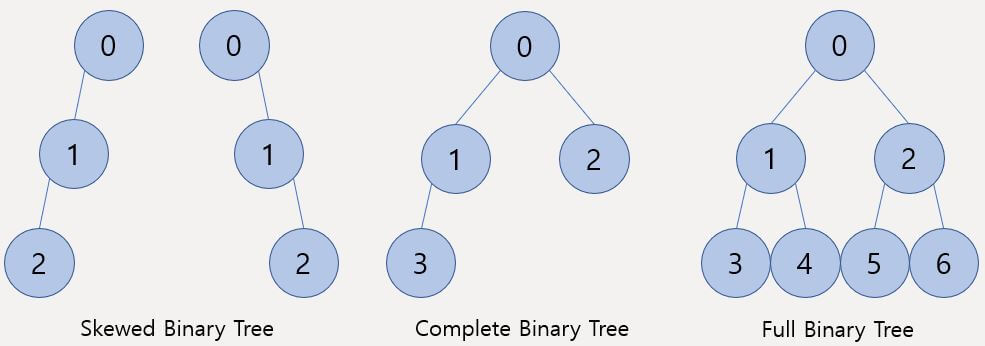
편향 트리(Skewed Binary Tree)는 모든 노드가 왼쪽 혹은 오른쪽 자식만 갖고 있는 형태이다.
완전 이진 트리(Complete Binary Tree)는 마지막 Level을 제외한 모든 Level의 노드가 완전히 채워져 있으며 마지막 Level의 노드들은 왼쪽부터 채워져 있는 형태이다.
포화 이진 트리(Full Binary Tree)는 완전 이진 트리에서 마지막 Level의 노드들도 채워져 있는, 즉 이진 트리가 보유할 수 있는 최대 노드를 가진 형태가 포화 이진 트리다.
이진 트리 순회 (Binary Tree Traversal)
이진 트리의 순회는 총 4가지가 있다.
- 전위 순회 (Pre-order)
- 중위 순회 (In-order)
- 후위 순회 (Post-order)
- 레벨 순회 (Level-order)
1번부터 3번까지는 왼쪽 서브 트리, 현재 노드, 오른쪽 서브 트리 중에 현재 노드를 언제 탐색하느냐에 따라 이름이 바뀌는 방식이고 레벨 순회는 루트 노드부터 같은 레벨인 노드를 차례로 탐색하는 방식이므로 너비 우선 순회(Breadth-first Traversal)라고도 한다.
따라서 전위 순회는 현재 -> 왼쪽 -> 오른쪽, 중위 순회는 왼쪽 -> 현재 -> 오른쪽, 후위 순회는 왼쪽 -> 오른쪽 -> 현재 순서로 방문하는 방식으로 단순하게 어느 지점에서 현재 노드를 출력하느냐의 차이일 뿐이다.
또한 레벨 순회는 그래프 탐색의 BFS(Breadth First Search)와 같이 큐를 사용하는 방법이므로 굳이 다루진 않겠다.
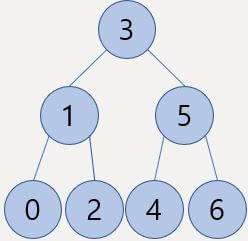
오른쪽과 같은 이진 트리를 예시로 들어보자.
순회를 하기 전에 조금 더 구체적인 설명을 하자면 루트인 3인 노드를 기준으로 왼쪽으로 내려가면 현재 노드가 1인 서브 트리, 오른쪽으로 내려가면 현재 노드가 5인 서브 트리로 생각할 수 있다.
각 서브 트리에서 다시 서브 트리로 내려갈 수 있는 구조이다.
즉, 전위 순회는 3->1->0->2->5->4->6, 중위 순회는 0->1->2->3->4->5->6, 후위 순회는 0->2->1->4->6->5->3 순으로 탐색하게 된다.
순회 구현
트리를 구현하는 방법은 다양하지만 자세한 건 이진 탐색 트리 포스팅에서 다루도록 하겠다.
이번 포스팅에서는 딕셔너리를 이용하여 구현했다.
딕셔너리의 키(Key)는 현재 노드의 값을 뜻하고 값(Value)은 길이가 2인 리스트로 선언하여 0번째 인덱스는 왼쪽 자식의 값, 1번째 인덱스는 오른쪽 자식의 값을 뜻한다.
이때 자식 노드가 없는 것을 표현하기 위해 '*'로 선언하여 숫자가 존재할 때만 해당 자식 노드로 이동하도록 구현하면 된다.
전체 코드를 통해 설명하겠다.
def preorder(root):
print(root,end=" ") #현재 노드 출력
if binary_tree[root][0]!="*": #왼쪽 자식 노드가 존재하면 이동
preorder(binary_tree[root][0])
if binary_tree[root][1]!="*": #오른쪽 자식 노드가 존재하면 이동
preorder(binary_tree[root][1])
def inorder(root):
if binary_tree[root][0]!="*":
inorder(binary_tree[root][0])
print(root,end=" ")
if binary_tree[root][1]!="*":
inorder(binary_tree[root][1])
def postorder(root):
if binary_tree[root][0]!="*":
postorder(binary_tree[root][0])
if binary_tree[root][1]!="*":
postorder(binary_tree[root][1])
print(root,end=" ")
root=3
binary_tree={3:[1,5],1:[0,2],0:['*','*'],2:['*','*'],5:[4,6],4:['*','*'],6:['*','*']}
print("전위 순회시작")
preorder(root)
print("\n\n중위 순회시작")
inorder(root)
print("\n\n전위 순회시작")
postorder(root)
구성을 보면 상당히 간단하단 것을 알 수 있다.
단순히 현재 노드의 값을 출력하는 부분이 어디에 위치하느냐에 따라 구분된다는 것을 알 수 있다.
따라서 한 가지를 이해하면 다른 것도 쉽기 때문에 Preorder로 설명하겠다.
시작은 루트부터 출발하여 각 함수의 매개변수로 넘겨준다.
해당 노드를 출력하고 만약 해당 노드의 왼쪽 자식 노드가 존재한다면 왼쪽 자식 노드의 값을 매개변수로 넘기고 재귀 호출한다.
그다음 오른쪽 자식 노드가 존재한다면 오른쪽 자식 노드의 값을 매개변수로 넘기고 재귀 호출한다면 알아서 반복하게 된다.

여기까지가 이진 트리에 대한 이론이지만 이를 실제 적용하기엔 다소 제한이 있다.
이진 트리를 직접 구현하여 사용하는 것은 이진 탐색 트리(Binary Search Tree)라고 하며 삽입과 삭제에 여러 가지 조건이 붙기 때문이다.
또한 트리도 사람마다 편한 방식이 다르기 때문에 다양한 구현 방법과 이진 탐색 트리의 작동 방식을 다음 포스팅에서 학습하도록 하겠다.
https://khsung0.tistory.com/26
[알고리즘] 이진 탐색 트리(Binary Search Tree) (Python)
설명 이진 탐색 트리(Binary Search Tree)란 왼쪽 서브 트리는 자신보다 작은 수들만 존재하고 오른쪽 서브 트리는 자신보다 큰 수들만 존재하는 이진트리를 뜻한다. 단순한 이진트리는 원하는 값의
khsung0.tistory.com
'알고리즘 > 자료구조 알고리즘 강의' 카테고리의 다른 글
| [알고리즘] 이진 탐색 트리(Binary Search Tree) (Python) (0) | 2021.12.18 |
|---|---|
| [자료구조] 힙(Heap) (Python) (0) | 2021.12.14 |
| [자료구조] 스택(Stack)과 큐(Queue) 데크(Deque)까지 (Python) (0) | 2021.12.04 |
| [알고리즘] 이진탐색 / 이분탐색 (Binary Search) (Python) (0) | 2021.12.02 |
| [PDF 전자책] 쉽게 풀어쓴 자료구조와 알고리즘 기본 가이드 (0) | 2021.11.27 |






